


Nächste Seite: Kompression bei der Temperatur
Aufwärts: Mischungen
Vorherige Seite: Kompression bei der Temperatur
Inhalt
Die Struktur bei der Temperatur T=1.25 wurde in dem Intervall der Dichte von
0.1 bis zur 0.66 mehrmals komprimiert und dekomprimiert. Mit den Strukturen bei
der Temperatur 1.25 wurden die meisten Simulationen durchgeführt, weil in
den Veröffentlichungen auf dem Gebiet von Simulationen mit dem GB Potential
gerade diese Temperatur sehr oft vorkommt. In diesem Unterkapitel wird nur ein
Teil der Ergebnisse vorgestellt, und zwar nur eine langsame Kompression, womit
wir Kompressionen bei allen fünf inbegriffenen Temperaturen (0.50, 0.75, 1.00,
1.25 und 1.50) vergleichen können. Der Rest der Ergebnisse wird in anderen
Unterkapiteln vorgestellt.
Bis zur Dichte 0.48 bildeten sich nur einzelne kleinere Domänen. Das System
war in der isotropischen Phase. Die Kompression in dem Intervall der Dichte
0.49-0.50 drängte die Domänen in eine globale Richtung. Die
Orientierungs-Ordnung wurde immer grösser und die nematische Phase wurde damit
ausgeprägter. Der Direktor nahm bei der Dichte  = 0.50 die Richtung
= 0.50 die Richtung
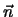 = (0.41, 0.88, 0.23) ein und man kann aus dem Schnappschüssen schon den
Entwurf für vier smektische Schichten sehen (Abbildung 4.14(a)
auf Seite
= (0.41, 0.88, 0.23) ein und man kann aus dem Schnappschüssen schon den
Entwurf für vier smektische Schichten sehen (Abbildung 4.14(a)
auf Seite ![[*]](cross_ref_motif.gif) ). Die nematische Phase ging bei weiterer
Kompression ab der Dichte 0.50 in die smektische Phase über. Der Prozess der
globalen Bildung von Schichten wurde bei der Dichte 0.51 abgeschlossen
(Abbildung 4.14(b) auf Seite
). Die nematische Phase ging bei weiterer
Kompression ab der Dichte 0.50 in die smektische Phase über. Der Prozess der
globalen Bildung von Schichten wurde bei der Dichte 0.51 abgeschlossen
(Abbildung 4.14(b) auf Seite ![[*]](cross_ref_motif.gif) ). Der
Direktor nahm bei der Dichte
). Der
Direktor nahm bei der Dichte  = 0.51 die Richtung
= 0.51 die Richtung
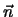 = (0.43, 0.82, 0.37)
ein. Es wurden wechselweise je fünf smektische Schichten gebildet. Die
zunehmende Orientierungsordnung die Kompression entlang zeigt sich in dem
Ordnungsparameter P2(1), der mit der Verdichtung auf dem Intervall der
Dichte 0.49-0.51 einen steilen Anstieg hat (Abbildung 4.21(a) auf
Seite
= (0.43, 0.82, 0.37)
ein. Es wurden wechselweise je fünf smektische Schichten gebildet. Die
zunehmende Orientierungsordnung die Kompression entlang zeigt sich in dem
Ordnungsparameter P2(1), der mit der Verdichtung auf dem Intervall der
Dichte 0.49-0.51 einen steilen Anstieg hat (Abbildung 4.21(a) auf
Seite ![[*]](cross_ref_motif.gif) ). Im Dichte-Intervall 0.51 bis 0.53 ordnen sich
vor allem die Teilchen innerhalb der Schichten ein. Der Direktor erhielt bei
der Dichte
). Im Dichte-Intervall 0.51 bis 0.53 ordnen sich
vor allem die Teilchen innerhalb der Schichten ein. Der Direktor erhielt bei
der Dichte  = 0.52 im wesentlichen die Richtung
= 0.52 im wesentlichen die Richtung
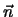 = (0.59, 0.76, 0.27)
(Abbildung 4.14(c) auf Seite
= (0.59, 0.76, 0.27)
(Abbildung 4.14(c) auf Seite ![[*]](cross_ref_motif.gif) ). Eine
weitere Kompression änderte an der Ordnung nicht viel. Bei der extrem hohen
Dichte
). Eine
weitere Kompression änderte an der Ordnung nicht viel. Bei der extrem hohen
Dichte  = 0.66 nahm der Direktor die Richtung
= 0.66 nahm der Direktor die Richtung
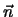 = (0.48, 0.74, 0.48)
ein. Auch die Schichten von kürzeren Teilchen wurden sehr deutlich
gebildet.
= (0.48, 0.74, 0.48)
ein. Auch die Schichten von kürzeren Teilchen wurden sehr deutlich
gebildet.
Für das System bei der Temperatur 1.25 werden hier nur die Graphen für die
Paarkorrelationsfunktionen für die Referenzteilchen (g(r), gl(r) und
gt(r)) an der linken Seite und die entsprechenden Graphen für die
Orientierungs-Paarkorrelationsfunktionen (g2(r), g2l(r) und
g2t(r)) an der rechten Seite vorgestellt.
Die Korrelationen für die Referenz-Teilchen weisen auf einen deutlichen
Übergang bei der Dichte 0.50 hin, wo der Übergang in die smektische Phase
stattfindet. Die Kompression entlang wurde vor allem die erste Amplitude für
die Paarkorrelationsfunktionen g[1](r) immer ausgeprägter, maximal 10.88 bei
der Dichte 0.66 (Abbildung 4.15(a) auf Seite
![[*]](cross_ref_motif.gif) ). Die verbliebenen Amplituden sind bei der
Dichte 0.66:
A2(1.76, 2.62),
A3(2.05, 1.90),
A4(2.70, 1.90),
A5(3.08, 1.44),
A6(3.65, 1.80) usw. Die Referenzteilchen besitzen in der
smektischen Phase ab der Dichte 0.52 eine lang reichende Raum-Ordnung. Der
Abstand, wo die erste Amplitude stattfindet, beträgt bis zur Dichte 0.53 immer
1.10. Die Amplitude beträgt dort 6.19. Bei den Dichten über 0.53 wird der
Abstand immer kleiner. Schliesslich beträgt er bei der Dichte 0.66 nur noch
1.02. Die entsprechenden Orientierungs-Paarkorrelationsfunktionen g2[1](r)
sind den Paarkorrelationsfunktionen g[1](r) sehr ähnlich, in der smektischen
Phase fast gleich. Das deutet auf einen extrem grossen Grad der
Orientierungsordnung hin.
). Die verbliebenen Amplituden sind bei der
Dichte 0.66:
A2(1.76, 2.62),
A3(2.05, 1.90),
A4(2.70, 1.90),
A5(3.08, 1.44),
A6(3.65, 1.80) usw. Die Referenzteilchen besitzen in der
smektischen Phase ab der Dichte 0.52 eine lang reichende Raum-Ordnung. Der
Abstand, wo die erste Amplitude stattfindet, beträgt bis zur Dichte 0.53 immer
1.10. Die Amplitude beträgt dort 6.19. Bei den Dichten über 0.53 wird der
Abstand immer kleiner. Schliesslich beträgt er bei der Dichte 0.66 nur noch
1.02. Die entsprechenden Orientierungs-Paarkorrelationsfunktionen g2[1](r)
sind den Paarkorrelationsfunktionen g[1](r) sehr ähnlich, in der smektischen
Phase fast gleich. Das deutet auf einen extrem grossen Grad der
Orientierungsordnung hin.
Die Longitudinal-Paarkorrelationsfunktionen gl[1](r) (Abbildung
4.15(b) auf Seite ![[*]](cross_ref_motif.gif) ) weisen ab der
Dichte 0.50 auf Schichten mit dem Abstand 3.14 hin. Die Amplituden sind höher
im Intervall der Dichte 0.53-0.59, wo die erste Amplitude von 2.75 bis 2.95
beträgt und die zweite von 2.78 bis 3.10. Es ist interessant, wie sich der
Abstand zwischen den Schichten die Kompression entlang verändert (Tabelle
4.4 auf Seite
) weisen ab der
Dichte 0.50 auf Schichten mit dem Abstand 3.14 hin. Die Amplituden sind höher
im Intervall der Dichte 0.53-0.59, wo die erste Amplitude von 2.75 bis 2.95
beträgt und die zweite von 2.78 bis 3.10. Es ist interessant, wie sich der
Abstand zwischen den Schichten die Kompression entlang verändert (Tabelle
4.4 auf Seite ![[*]](cross_ref_motif.gif) ). Der Abstand wird nämlich
mit der zunehmender Dichte nicht immer kleiner, sondern ab und zu auch
grösser, was aus den globalen Änderungen der Struktur stammt. In einem extrem
dichten System werden sowohl die Amplituden als auch die Abstände zwischen den
Amplituden kleiner, weil die Verdichtung die Neigung der Teilchen innerhalb der
Schichten verursacht. Die entsprechenden
Longitudinal-Orientierungs-Paarkorrelationsfunktionen
g2l[1](r) sind den
gl[1](r) wieder sehr ähnlich, nur etwas niedriger.
). Der Abstand wird nämlich
mit der zunehmender Dichte nicht immer kleiner, sondern ab und zu auch
grösser, was aus den globalen Änderungen der Struktur stammt. In einem extrem
dichten System werden sowohl die Amplituden als auch die Abstände zwischen den
Amplituden kleiner, weil die Verdichtung die Neigung der Teilchen innerhalb der
Schichten verursacht. Die entsprechenden
Longitudinal-Orientierungs-Paarkorrelationsfunktionen
g2l[1](r) sind den
gl[1](r) wieder sehr ähnlich, nur etwas niedriger.
Tabelle 4.4:
Der Abstand zwischen den Schichten bei bestimmten
Dichten.
|
|
Dichte |
0.50 |
0.51 |
0.52 |
0.53 |
0.54 |
0.55 |
0.56 |
0.57 |
0.58 |
0.59 |
0.60 |
0.66 |
|
Abstand |
3.14 |
3.14 |
3.29 |
3.20 |
3.25 |
3.18 |
3.16 |
3.12
|
3.08 |
3.06 |
3.09 |
2.97 |
|
Die Transversal-Paarkorrelationsfunktionen gt[1](r) (Abbildung
4.15(c) auf Seite ![[*]](cross_ref_motif.gif) ) zeigen erst
bei den Dichten ab 0.55 eine lang reichende Raum-Ordnung. Die Amplituden sind
bei höherer Dichte nicht immer grösser, sondern oszillieren auch mit
zunehmender Dichte. Besonders ausgeprägt ist die erste Amplitude bei den
Dichten 0.58 (4.81) und 0.61 (4.82). Die Oszillationen weisen darauf hin, dass
es auch zwischen den Schichten wegen der Kompression einige Veränderungen in
der Korrelation gibt. Die zweite Amplitude hat die Kompression entlang etwas
glatteren Verlauf und beträgt ab der Dichte 0.55 ungefähr 3. Die verbliebenen
Amplituden betragen bis zu 1.4 und weisen auf eine lang reichende Raumordnung
hin. Wieder sind die entsprechenden
Transversal-Orientierungs-Paarkorrelationsfunktionen
g2t[1](r) ab der
Dichte 0.50 wegen des hohen Orientierung-Grades den
gt[1](r) sehr
ähnlich.
) zeigen erst
bei den Dichten ab 0.55 eine lang reichende Raum-Ordnung. Die Amplituden sind
bei höherer Dichte nicht immer grösser, sondern oszillieren auch mit
zunehmender Dichte. Besonders ausgeprägt ist die erste Amplitude bei den
Dichten 0.58 (4.81) und 0.61 (4.82). Die Oszillationen weisen darauf hin, dass
es auch zwischen den Schichten wegen der Kompression einige Veränderungen in
der Korrelation gibt. Die zweite Amplitude hat die Kompression entlang etwas
glatteren Verlauf und beträgt ab der Dichte 0.55 ungefähr 3. Die verbliebenen
Amplituden betragen bis zu 1.4 und weisen auf eine lang reichende Raumordnung
hin. Wieder sind die entsprechenden
Transversal-Orientierungs-Paarkorrelationsfunktionen
g2t[1](r) ab der
Dichte 0.50 wegen des hohen Orientierung-Grades den
gt[1](r) sehr
ähnlich.
Abbildung:
Schnappschüsse für die äquimolaren Mischungen bei T=1.25.
![\begin{figure}
\begin{center}
\subfigure [T=1.25, $\rho=$\ 0.50]
{\mbox{\epsfig ...
...fig {file=fig/lex315t125r052.elview.ps, height=5.3cm}}}
\end{center}\end{figure}](img179.gif) |
Abbildung:
Korrelationsfunktionen für die äquimolaren Mischungen bei
T=1.25.
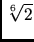 |



Nächste Seite: Kompression bei der Temperatur
Aufwärts: Mischungen
Vorherige Seite: Kompression bei der Temperatur
Inhalt
Renato Lukac
2000-01-02
![[*]](cross_ref_motif.gif) ). Die nematische Phase ging bei weiterer
Kompression ab der Dichte 0.50 in die smektische Phase über. Der Prozess der
globalen Bildung von Schichten wurde bei der Dichte 0.51 abgeschlossen
(Abbildung 4.14(b) auf Seite
). Die nematische Phase ging bei weiterer
Kompression ab der Dichte 0.50 in die smektische Phase über. Der Prozess der
globalen Bildung von Schichten wurde bei der Dichte 0.51 abgeschlossen
(Abbildung 4.14(b) auf Seite ![[*]](cross_ref_motif.gif) ). Der
Direktor nahm bei der Dichte
). Der
Direktor nahm bei der Dichte ![[*]](cross_ref_motif.gif) ). Im Dichte-Intervall 0.51 bis 0.53 ordnen sich
vor allem die Teilchen innerhalb der Schichten ein. Der Direktor erhielt bei
der Dichte
). Im Dichte-Intervall 0.51 bis 0.53 ordnen sich
vor allem die Teilchen innerhalb der Schichten ein. Der Direktor erhielt bei
der Dichte ![[*]](cross_ref_motif.gif) ). Eine
weitere Kompression änderte an der Ordnung nicht viel. Bei der extrem hohen
Dichte
). Eine
weitere Kompression änderte an der Ordnung nicht viel. Bei der extrem hohen
Dichte