


Nächste Seite: Mischungen von Gay-Berne Teilchen
Aufwärts: Mischungen
Vorherige Seite: Vorversuch 1: Mischungen von
Inhalt
Die Flüssigkeitsmischungen kann man auf verschiedene Arten simulieren. Wir
haben uns entschieden einige einfache Vorversuche durchzuführen. Das
Lennard-Jones (LJ) Potential (Gleichung 2.1 auf Seite
![[*]](cross_ref_motif.gif) ) [41,42] dient schon seit Jahrzehnte für die
mathematische Beschreibung der Interaktion von isotropen Moleküle. Auch das
GB Potential ist, wie wir schon früher erwähnt haben, im Grunde ein
modifiziertes LJ Potential. Um die Mischungsparameter und den Einfluss der
Mischungstechnik zu testen, haben wir zweidimensionale Monte Carlo Experimente
an Mischungen von LJ Flüssigkeiten durchgeführt [49]. Die 1024
Moleküle teilten wir in zwei Typen ein, je 512 Moleküle. Der erste Typ wurde
mit
) [41,42] dient schon seit Jahrzehnte für die
mathematische Beschreibung der Interaktion von isotropen Moleküle. Auch das
GB Potential ist, wie wir schon früher erwähnt haben, im Grunde ein
modifiziertes LJ Potential. Um die Mischungsparameter und den Einfluss der
Mischungstechnik zu testen, haben wir zweidimensionale Monte Carlo Experimente
an Mischungen von LJ Flüssigkeiten durchgeführt [49]. Die 1024
Moleküle teilten wir in zwei Typen ein, je 512 Moleküle. Der erste Typ wurde
mit
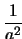 und
und
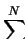 in dem LJ Potential beschrieben, der zweite
mit
in dem LJ Potential beschrieben, der zweite
mit
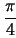 und
und
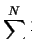 . Die Interaktion zwischen Teilchen
verschiedenen Typs wurde mit
. Die Interaktion zwischen Teilchen
verschiedenen Typs wurde mit
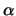 und
und
 beschrieben. Das Zeichen Asterix (*) bei den Namen bezieht sich auf das LJ
Potential.
beschrieben. Das Zeichen Asterix (*) bei den Namen bezieht sich auf das LJ
Potential.
Wir haben folgende Parametrisierung eingeführt:
 = =  , , 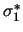 = = 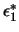 , , 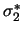 = = 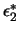 , , 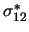 = = 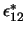 , , 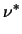 = = 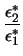 , , 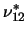 = = 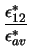 . .
|
(4.4) |
Um den Einfluss der Technik deutlicher zu verstehen, haben wir jeweils einen
von den Parametern auf einen grösseren Wert gesetzt. Wir haben nach langer
Thermalization bei der Temperatur T=1 und der Dichte
 = 0.6 die Struktur
visuell betrachtet. Die Teilchen des ersten Typs sind im rot dargestellt, des
zweiten Typs im grün. Der Parameter
= 0.6 die Struktur
visuell betrachtet. Die Teilchen des ersten Typs sind im rot dargestellt, des
zweiten Typs im grün. Der Parameter 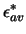 gibt die Tiefe des LJ Potentials
für die Interaktion zwischen den Teilchen des zweiten Typs im Vergleich zur
1-1 Wechselwirkung an. Die Konfiguration für
gibt die Tiefe des LJ Potentials
für die Interaktion zwischen den Teilchen des zweiten Typs im Vergleich zur
1-1 Wechselwirkung an. Die Konfiguration für 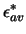 = 3 zeigt keine
wesentlichen Änderungen (Abbildung 4.4(b) auf Seite
= 3 zeigt keine
wesentlichen Änderungen (Abbildung 4.4(b) auf Seite
![[*]](cross_ref_motif.gif) ) im Vergleich mit der Referenz (Abbildung
4.4(a) auf Seite
) im Vergleich mit der Referenz (Abbildung
4.4(a) auf Seite ![[*]](cross_ref_motif.gif) ), obwohl sich die Moleküle
des zweiten Typs bei dieser Parametrisierung zum 'Zusammenballen' weigern. Als
nächstes wurde nur die Tiefe des Potentials zwischen den Teilchen
verschiedener Typen auf
), obwohl sich die Moleküle
des zweiten Typs bei dieser Parametrisierung zum 'Zusammenballen' weigern. Als
nächstes wurde nur die Tiefe des Potentials zwischen den Teilchen
verschiedener Typen auf
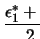 = 5 getestet. Die Parametrisierung
entspricht einer starken Tendenz für Mischung, was sich auch in einer besser
gemischten Struktur widerspiegelt (Abbildung 4.4(c) auf Seite
= 5 getestet. Die Parametrisierung
entspricht einer starken Tendenz für Mischung, was sich auch in einer besser
gemischten Struktur widerspiegelt (Abbildung 4.4(c) auf Seite
![[*]](cross_ref_motif.gif) ). Dann wurde mit verschiedenen Durchmessern
experimentiert. Die grösseren Teilchen haben sich bei dem Parameter
). Dann wurde mit verschiedenen Durchmessern
experimentiert. Die grösseren Teilchen haben sich bei dem Parameter 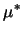 = 3
gleichmässig verteilt und bei etwas grösserer Dichte (
= 3
gleichmässig verteilt und bei etwas grösserer Dichte (
 = 0.6) die
kleinen Referenzteilchen in kleine Domänen gedrängt (Abbildung
4.4(d) auf Seite
= 0.6) die
kleinen Referenzteilchen in kleine Domänen gedrängt (Abbildung
4.4(d) auf Seite ![[*]](cross_ref_motif.gif) ). Noch deutlicher wurden die
Domänen der Teilchen eines Typs bei dem Parameter
). Noch deutlicher wurden die
Domänen der Teilchen eines Typs bei dem Parameter
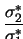 = 3 (Abbildung
4.4(e) auf Seite
= 3 (Abbildung
4.4(e) auf Seite ![[*]](cross_ref_motif.gif) ). Obwohl dabei alle
Teilchen gleich gross sind, verlangte die Parametrisierung von den Teilchen
verschiedener Typen eine dreimal grössere Distanz als zwischen den Teilchen
des gleichen Typs.
). Obwohl dabei alle
Teilchen gleich gross sind, verlangte die Parametrisierung von den Teilchen
verschiedener Typen eine dreimal grössere Distanz als zwischen den Teilchen
des gleichen Typs.
Wir können aus den Abbildungen entnehmen, das der Einfluss der Parametern
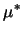 und
und
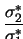 viel grösser ist als von
viel grösser ist als von 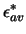 und
und
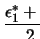 .
Die Distanz, bei der das Minimum des Potentials liegt, ist wichtiger als seine
Tiefe. Auch die Temperatur und die Dichte sind wichtig, was uns die
letzte Konfiguration aus dieser Serie sehr deutlich darstellt (Abbildung
4.4(f) auf Seite
.
Die Distanz, bei der das Minimum des Potentials liegt, ist wichtiger als seine
Tiefe. Auch die Temperatur und die Dichte sind wichtig, was uns die
letzte Konfiguration aus dieser Serie sehr deutlich darstellt (Abbildung
4.4(f) auf Seite ![[*]](cross_ref_motif.gif) ). Die Parametrisierung
). Die Parametrisierung
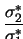 = 3,
= 3, 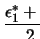 = 1.5 verursachte die Bildung der leeren
Streifen zwischen den Domänen der Moleküle denselben Typs. Die Verdichtung des
Systems führt nur zur Vereinigung von vielen Domänen in grössere globale
Domänen mit ausgeprägten Streifen dazwischen.
= 1.5 verursachte die Bildung der leeren
Streifen zwischen den Domänen der Moleküle denselben Typs. Die Verdichtung des
Systems führt nur zur Vereinigung von vielen Domänen in grössere globale
Domänen mit ausgeprägten Streifen dazwischen.
Wir haben mit den zweidimensionalen LJ-Mischungen den Einfluss der
Mischungsparameter getestet und anhand der Ergebnisse für
Mischungen von FK mit verschiedener Länge entschieden.
Abbildung:
Die Lennard-Jones Strukturen für verschiedene Mischungsparameter.
Genannt sind nur die Parameter, die nicht gleich 1 sind. Die Temperatur und die
Dichte sind für die letzte Struktur T=1.5 und
 = 0.7, sonst aber immer
T=1.0 und
= 0.7, sonst aber immer
T=1.0 und
 = 0.6 [49].
= 0.6 [49].
![\begin{figure}
\begin{center}
\subfigure [$die Referenz$]
{\mbox{\epsfig {file=...
...fig {file=fig/ljmix61a.ps, height=4.5cm, width=4.5cm}}}
\end{center}\end{figure}](img159.gif) |



Nächste Seite: Mischungen von Gay-Berne Teilchen
Aufwärts: Mischungen
Vorherige Seite: Vorversuch 1: Mischungen von
Inhalt
Renato Lukac
2000-01-02
![[*]](cross_ref_motif.gif) ) [41,42] dient schon seit Jahrzehnte für die
mathematische Beschreibung der Interaktion von isotropen Moleküle. Auch das
GB Potential ist, wie wir schon früher erwähnt haben, im Grunde ein
modifiziertes LJ Potential. Um die Mischungsparameter und den Einfluss der
Mischungstechnik zu testen, haben wir zweidimensionale Monte Carlo Experimente
an Mischungen von LJ Flüssigkeiten durchgeführt [49]. Die 1024
Moleküle teilten wir in zwei Typen ein, je 512 Moleküle. Der erste Typ wurde
mit
) [41,42] dient schon seit Jahrzehnte für die
mathematische Beschreibung der Interaktion von isotropen Moleküle. Auch das
GB Potential ist, wie wir schon früher erwähnt haben, im Grunde ein
modifiziertes LJ Potential. Um die Mischungsparameter und den Einfluss der
Mischungstechnik zu testen, haben wir zweidimensionale Monte Carlo Experimente
an Mischungen von LJ Flüssigkeiten durchgeführt [49]. Die 1024
Moleküle teilten wir in zwei Typen ein, je 512 Moleküle. Der erste Typ wurde
mit