


Nächste Seite: Observablen: Ordnungsparameter, Druck und
Aufwärts: Computersimulationen und Modellpotential für
Vorherige Seite: Die Methode: Monte Carlo
Inhalt
Die ersten Simulationen auf der molekularen Ebene wurden mit Gittermodellen
durchgeführt. Die Spins, die kleinere Domänen von Molekülen mit gleicher
Orientierung darstellen, werden dabei auf ein Gitter verteilt und interagieren
miteinander mit einen Potential, wie zum Beispiel dem nach Lebwohl-Lasher
Ui, j = 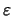 P2(cos
P2(cos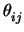 )[30,31], das eigentlich die
mikroskopische Variante des Maier-Saupe Potentials [32,33,34] aus der
Kontinuumtheorie ist, und dass einen Übergang
isotropisch-nematisch darstellt. Wegen seiner einfachen Form wurden viele
umfangreiche Studien mit diesem Potential durchgeführt, wie z.B.
Phasenübergänge [35,36], Grenzflächen [37,38], elastische
[39] und optische Eigenschaften [40] usw.
)[30,31], das eigentlich die
mikroskopische Variante des Maier-Saupe Potentials [32,33,34] aus der
Kontinuumtheorie ist, und dass einen Übergang
isotropisch-nematisch darstellt. Wegen seiner einfachen Form wurden viele
umfangreiche Studien mit diesem Potential durchgeführt, wie z.B.
Phasenübergänge [35,36], Grenzflächen [37,38], elastische
[39] und optische Eigenschaften [40] usw.
Es gibt auch viele Experimente mit harten Potentialen (Ellipsoiden,
Sphärozylindern, Plättchen etc.) [4,5,6,7,8], doch ein
weiches Modell ist nützlicher, weil es neben einer kurz reichenden Abstossung
noch einen weitreichenden Anziehungsanteil hat. Ein seit längerer Zeit
bekanntes Modell für die isotropen Moleküle ist das Lennard-Jones Potential
[41,42]:
das eine Wechselwirkung zwischen zwei Kugeln darstellt und
somit für Argon ideal ist. Im Jahr 1972 entwarfen B.J.Berne und P.Pechukas
[43] das sogenannte 'Gaussian Overlap Potential'. Das war eigentlich ein
modifiziertes Lennard-Jones Potential, mit dem man längliche (ellipsoidische)
Moleküle darstellen konnte. J.G.Gay und B.J.Berne verbesserten es neun Jahre
später [44] und erst Ende der Achtzigerjahre führte G.R.Luckhurst
mehrere genaue Untersuchungen durch [45,46].
Das Gay-Berne Potential hat die Form [43,44]:
wobei
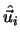 und
und
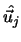 die Einheitsvektoren in
der Richtung der Moleküle i und j sind,
die Einheitsvektoren in
der Richtung der Moleküle i und j sind,
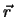 =
= 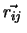 ist der intermolekulare Vektor (Abbildung 2.2 auf Seite
ist der intermolekulare Vektor (Abbildung 2.2 auf Seite
![[*]](cross_ref_motif.gif) ).
).
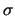 (
(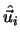 ,
,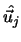 ,
,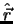 ) ist gegeben durch:
) ist gegeben durch:
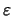 (
(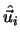 ,
,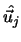 ,
,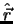 ) bestimmt die
Tiefe des Potentials:
) bestimmt die
Tiefe des Potentials:
wobei
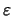 (
(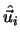 ,
,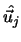 ) und
) und
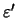 (
(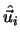 ,
,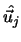 ,
,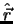 )
seine Parameter sind:
)
seine Parameter sind:
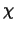 ist der Anisotropie - Parameter des Durchmessers:
ist der Anisotropie - Parameter des Durchmessers:
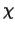 = = 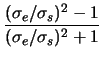 , ,
|
(2.7) |
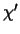 ist der Anisotropie - Parameter der Potentialtiefe:
ist der Anisotropie - Parameter der Potentialtiefe:
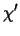 = = 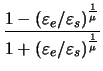 . .
|
(2.8) |
Mit der Parametrisierung des Potentials haben sich mehrere Forscher
beschäftigt [46,47,48,49], besonders hinsichtlich der Parameter
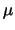 und
und 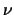 . Es hat sich erwiesen, dass die günstigste Kombination für
FK lautet [50]:
. Es hat sich erwiesen, dass die günstigste Kombination für
FK lautet [50]:
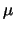 = 2, = 2, 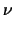 = 1, = 1,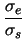 = 3,tex2html_image_mark>#tex2html_wrap_indisplay9818#� = = 3,tex2html_image_mark>#tex2html_wrap_indisplay9818#� = 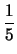 , ,
|
(2.9) |
was auch uns als Grundlage diente. Wegen der Einfachheit bezeichnen wir den
Quotient
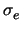 /
/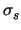 nur mit
nur mit 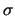 und ebenso
und ebenso
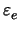 /
/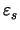 mit
mit
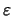 . Die oben angeführte Parametrisierung
ergibt ein reiches Phasendiagramm (Abbildung 2.2 auf Seite
. Die oben angeführte Parametrisierung
ergibt ein reiches Phasendiagramm (Abbildung 2.2 auf Seite
![[*]](cross_ref_motif.gif) ) von der isotropischen über die nematische bis zur
smektischen Phase [50,51].
) von der isotropischen über die nematische bis zur
smektischen Phase [50,51].
Abbildung:
Richtung der Moleküle und der intermolekulare Vektor.
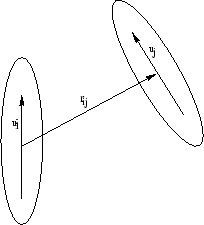 |
Abbildung:
GB-Potential für den Reinstoff der Länge 3 (
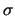 = 3).
= 3).
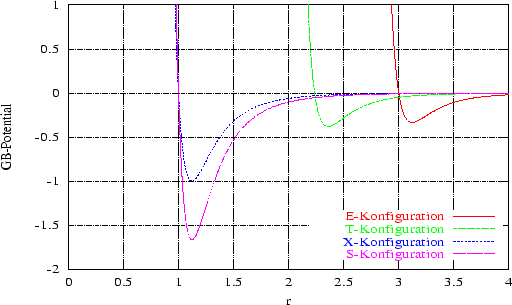 |
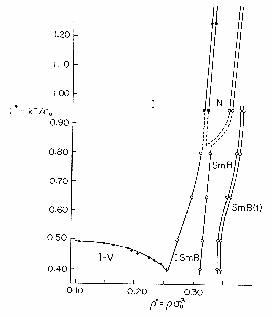
Abbildung:
GB-Phasendiagramm für den Reinstoff der Länge 3 (
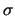 = 3)
[50].
= 3)
[50].
 |



Nächste Seite: Observablen: Ordnungsparameter, Druck und
Aufwärts: Computersimulationen und Modellpotential für
Vorherige Seite: Die Methode: Monte Carlo
Inhalt
Renato Lukac
2000-01-02
![]() P2(cos
P2(cos![]() )[30,31], das eigentlich die
mikroskopische Variante des Maier-Saupe Potentials [32,33,34] aus der
Kontinuumtheorie ist, und dass einen Übergang
isotropisch-nematisch darstellt. Wegen seiner einfachen Form wurden viele
umfangreiche Studien mit diesem Potential durchgeführt, wie z.B.
Phasenübergänge [35,36], Grenzflächen [37,38], elastische
[39] und optische Eigenschaften [40] usw.
)[30,31], das eigentlich die
mikroskopische Variante des Maier-Saupe Potentials [32,33,34] aus der
Kontinuumtheorie ist, und dass einen Übergang
isotropisch-nematisch darstellt. Wegen seiner einfachen Form wurden viele
umfangreiche Studien mit diesem Potential durchgeführt, wie z.B.
Phasenübergänge [35,36], Grenzflächen [37,38], elastische
[39] und optische Eigenschaften [40] usw.
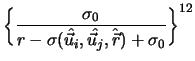 -
- 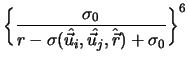
![[*]](cross_ref_motif.gif) ).
).
![$\displaystyle {\Biggl[1-{1 \over
2}\chi\biggl\{
{{(\hat{\vec{r}}\cdot\hat{\vec{...
...1-\chi(\hat{\vec{u}_i}\cdot\hat{\vec{u}_j})}
\biggr\}\Biggr]}^{-{1 \over 2}}_{}$](img45.gif) ,
,
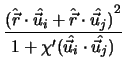 +
+ 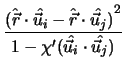
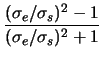 ,
,
![[*]](cross_ref_motif.gif) ) von der isotropischen über die nematische bis zur
smektischen Phase [50,51].
) von der isotropischen über die nematische bis zur
smektischen Phase [50,51].