Q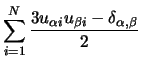 . .
|
(2.10) |
Die Orientierungsordnung wird bei den FK auf dem mikroskopischen Niveau meistens durch den Ordnungsparameter P2 beschrieben. Man erhält ihn als den grössten Eigenwert des Q Tensors [27,52]:
Q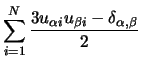 . .
|
(2.10) |
Wir haben für die Mischungen separat P2 für jede Struktur berechnet, und
zwar P2(1) für die erste Teilchensorte, bzw. P2(2) für die zweiten
Teilchen, und noch für das komplette System P2. Durch den
Ordnungsparameter konnten wir den Grad der Orientierungsordnung und damit die Phase
für jede Teilchenart bestimmen.
Eine besonders wichtige Rolle spielt bei den FK der Direktor. Er ergibt sich
als Eigenvektor, der dem grössten Eigenwert des Q entspricht. Er zeigt in die
Richtung der dominanten Orientierung.
Bei der Visualisierung wurde die Richtung des Direktors in den meisten
Fällen als eine lange Linie eingezeichnet. Der Blickwinkel bei der 3D
Visualisierung wurde so bestimmt, dass der Direktor in der Ebene der 2D
Projektion lag. Damit waren die Domänen und die smektischen Schichten
besonders deutlich zu sehen.
Der Druck wurde nach dem Virialsatz bestimmt [28]:
p = 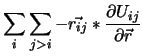 . .
|
(2.11) |
Die Dichte des Systems ist mit der Anzahl der Teilchen N und dem Volumen V definiert:
|
|
(2.12) |
Die dritte wichtige Observable war die Energie pro Teilchen. Sie wurde in unserem Fall als der Mittelwert von der gesamten potentiellen Energie des Systems errechnet [28]:
|
E = |
(2.13) |
Für alle Observablen wurde zuerst eine Datei erstellt, die die Werte die
Kompression oder die Kühlung entlang beschrieb. Mit diesen Daten wurde dann
die Statistik gemacht, so dass jeder Punkt an den Kurven als ein Durchschnitt
von 50 bis 100 Daten ist. An den Graphen ist für jeden Punkt auch der Fehler
eingezeichnet, der mit Statistik bestimmt wurde. Alle Graphen, auch für die
Korrelationen und fürs Potential, wurden mit dem Programm GNUPLOT unter LINUX
hergestellt. Die Graphen für das GB-Potential wurden für vier Orientierungen
gezeichnet (Abbildung 2.4 auf Seite ![[*]](cross_ref_motif.gif) ). Mit S/E
wurde der Quotient zwischen den Minima der S- und E-Konfiguration bezeichnet
und die weiteren Quotienten dann nach demselben Prinzip: S/X, S/T, X/T, X/E
und T/E.
). Mit S/E
wurde der Quotient zwischen den Minima der S- und E-Konfiguration bezeichnet
und die weiteren Quotienten dann nach demselben Prinzip: S/X, S/T, X/T, X/E
und T/E.
Wir haben reduzierte Variablen mit entsprechenden Einheiten verwendet
[27,28]:
ro = ![]() (Länge)
(Länge)
Eo = ![]() (Energie)
(Energie)
To = ![]() /k (Temperatur)
/k (Temperatur)
![]() = 1/
= 1/![]() (Dichte)
(Dichte)
po = ![]() /
/![]() (Druck)
(Druck)
Wir haben für die 3D-Visualisierung ein Programm in C++ verfasst
(GB-plot), das die Teilchen mit kleinen Linien darstellt. Bei den Mischungen
wurde dafür ausserdem noch das Programm elview von Prof.Dr. M.Neumann
verwendet.