


Nächste Seite: Teilchen der Länge 4.0
Aufwärts: GB-Reinstoffe
Vorherige Seite: Teilchen der Länge 3.0
Inhalt
Die Länge 3.5 ist gut geeignet für die Darstellung von FK und wurde schon oft
bei den Mischungen verwendet [13,14]. Die Minima des Potentials für die
E- und T-Konfiguration sind auch hier mit einem bestimmten Abstand deutlich
unter den anderen zwei Kurven (Abbildung 3.18 auf Seite
![[*]](cross_ref_motif.gif) ). Für die E-Konfiguration liegt das Minimum bei dem
Abstand 3.62 und beträgt -0.378. Das ist fast 20 mal tiefer als das
Potential für die T-Konfiguration (-0.021), mehr als 100 mal tiefer als die
S-Konfiguration (-0.003) und die X-Konfiguration (-0.002) und zwar bei dem
Abstand 3.62. Bei dem Abstand 2.70 beträgt das Minimum für die
T-Konfiguration -0.382. Das Potential ist dort ungefähr 20 mal, bzw.
40 mal tiefer als die übrigen zwei Orientierungen (S-Konfiguration:
-0.020, X-Konfiguration: -0.010), die aber ihre Minima bei dem Abstand 1.12
haben (X-Konfiguration -1.00 und S-Konfiguration -1.893). Wenn wir nur die
Tiefe der Minima vergleichen, dann sehen wir, dass die Minima der S- und
X-Konfiguration 2.5 bis zu 5 mal grösser sind als die Minima der E- und
T-Konfiguration, wobei die letzten zwei fast gleich sind (S/X=1.89, S/T=4.96,
S/E=5.00, X/T=2.62, X/E=2.64, T/E=1.01).
). Für die E-Konfiguration liegt das Minimum bei dem
Abstand 3.62 und beträgt -0.378. Das ist fast 20 mal tiefer als das
Potential für die T-Konfiguration (-0.021), mehr als 100 mal tiefer als die
S-Konfiguration (-0.003) und die X-Konfiguration (-0.002) und zwar bei dem
Abstand 3.62. Bei dem Abstand 2.70 beträgt das Minimum für die
T-Konfiguration -0.382. Das Potential ist dort ungefähr 20 mal, bzw.
40 mal tiefer als die übrigen zwei Orientierungen (S-Konfiguration:
-0.020, X-Konfiguration: -0.010), die aber ihre Minima bei dem Abstand 1.12
haben (X-Konfiguration -1.00 und S-Konfiguration -1.893). Wenn wir nur die
Tiefe der Minima vergleichen, dann sehen wir, dass die Minima der S- und
X-Konfiguration 2.5 bis zu 5 mal grösser sind als die Minima der E- und
T-Konfiguration, wobei die letzten zwei fast gleich sind (S/X=1.89, S/T=4.96,
S/E=5.00, X/T=2.62, X/E=2.64, T/E=1.01).
Abbildung:
GB Potential für den Reinstoff der Länge 3.5.
 |
Das System wurde bei der Anfangsdichte  = 0.08 und Temperatur 1.25
thermalisiert. Mit diesem Ergebnis wurde in zwei Richtungen simuliert: das
erste System wurde bis T=0.50 gekühlt, das zweite wurde bis T=1.50 erhitzt.
Die Kompressionen folgten bei den Temperaturen T=0.50, T=0.75, T=1.0, 1.25
und T=1.50 bis zur Maximaldichte
= 0.08 und Temperatur 1.25
thermalisiert. Mit diesem Ergebnis wurde in zwei Richtungen simuliert: das
erste System wurde bis T=0.50 gekühlt, das zweite wurde bis T=1.50 erhitzt.
Die Kompressionen folgten bei den Temperaturen T=0.50, T=0.75, T=1.0, 1.25
und T=1.50 bis zur Maximaldichte  = 0.32. Die Visualisierung (Abbildung
3.19 auf Seite
= 0.32. Die Visualisierung (Abbildung
3.19 auf Seite ![[*]](cross_ref_motif.gif) ) zeigt nicht nur die Bildung von
Schichten für den Übergang bei den Temperaturen 0.5 und 1.00 sondern auch die
Orientierung der Teilchen ohne Bildung von Schichten bei der Temperatur 1.50.
Der Schnappschuss bei der niedrigsten Temperatur (a-c) stellt deutlich dar, wie
sich in der Mitte noch eine Schichte der Teilchen bildet. Bei der Temperatur
0.5 nimmt der Direktor im Lauf der Kompression die Richtung
) zeigt nicht nur die Bildung von
Schichten für den Übergang bei den Temperaturen 0.5 und 1.00 sondern auch die
Orientierung der Teilchen ohne Bildung von Schichten bei der Temperatur 1.50.
Der Schnappschuss bei der niedrigsten Temperatur (a-c) stellt deutlich dar, wie
sich in der Mitte noch eine Schichte der Teilchen bildet. Bei der Temperatur
0.5 nimmt der Direktor im Lauf der Kompression die Richtung
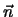 = (0.78, 0.28, 0.56)
= (0.78, 0.28, 0.56) 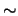
 (3/1/2) ein. Das System hat
eine isotrope
(
(3/1/2) ein. Das System hat
eine isotrope
( < 0.18) und eine smektische Phase
(
< 0.18) und eine smektische Phase
( > 0.23).
Dazwischen
(0.18 <
> 0.23).
Dazwischen
(0.18 <  < 0.23) ist eine 'Meta-Phase', wobei ein Teil in
der isotropen und der Rest in der smektischen Phase ist. Der Schnappschuss bei
der Temperatur 1.0 (d-f) stellt drei Phasen dar. Bei genügend niedriger
Dichte
(
< 0.23) ist eine 'Meta-Phase', wobei ein Teil in
der isotropen und der Rest in der smektischen Phase ist. Der Schnappschuss bei
der Temperatur 1.0 (d-f) stellt drei Phasen dar. Bei genügend niedriger
Dichte
( < 0.23) gibt es eine isotrope Phase. Bei Kompression
(0.23 <
< 0.23) gibt es eine isotrope Phase. Bei Kompression
(0.23 <  < 0.25) geht das System in eine nematische Phase
(0.25 <
< 0.25) geht das System in eine nematische Phase
(0.25 <  < 0.28)
und schliesslich
(0.28 <
< 0.28)
und schliesslich
(0.28 <  < 0.29) noch in eine smektische Phase
(
< 0.29) noch in eine smektische Phase
( > 0.29) über mit dem Direktor in der Richtung
> 0.29) über mit dem Direktor in der Richtung
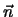 = (0.04, 0.60, 0.80)
= (0.04, 0.60, 0.80) 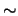
 (0/3/4). Der Schnappschuss bei der Temperatur 1.5 (g-i) zeigt das
System in einer isotropen
(
(0/3/4). Der Schnappschuss bei der Temperatur 1.5 (g-i) zeigt das
System in einer isotropen
( < 0.24) und einer nematischen Phase
(
< 0.24) und einer nematischen Phase
( > 0.26) mit den Direktor in der Richtung
> 0.26) mit den Direktor in der Richtung
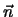 = (0.37, - 0.03, 0.93)
= (0.37, - 0.03, 0.93) 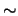
 (1/0/3). Wenn die Kompression zu rasch durchgeführt wird,
dann kann sich dieser Prozess nicht einstellen. Bei einer höheren Temperatur
geschieht der Übergang bei einer höheren Dichte, daher ist der Abstand
zwischen den Schichten kleiner - die Schichten wurden näher aneinander
gepresst. Bei einer genügend hohen Temperatur würde der Abstand dann zu
klein. Die Abstossung zwischen den Schichten würde zu gross, deswegen gibt es
einen anderen Kompromiss, bei dem es keine Schichten gibt.
(1/0/3). Wenn die Kompression zu rasch durchgeführt wird,
dann kann sich dieser Prozess nicht einstellen. Bei einer höheren Temperatur
geschieht der Übergang bei einer höheren Dichte, daher ist der Abstand
zwischen den Schichten kleiner - die Schichten wurden näher aneinander
gepresst. Bei einer genügend hohen Temperatur würde der Abstand dann zu
klein. Die Abstossung zwischen den Schichten würde zu gross, deswegen gibt es
einen anderen Kompromiss, bei dem es keine Schichten gibt.
Abbildung:
Schnappschüsse für den Reinstoff der Länge 3.5.
![\begin{figure}
\begin{center}
\subfigure [T=0.50, $\rho=$\ 0.17]
{\mbox{\epsfig ...
...{\mbox{\epsfig {file=fig/l35t150r031.ps, width=4.5cm}}}
\end{center}\end{figure}](img129.gif) |
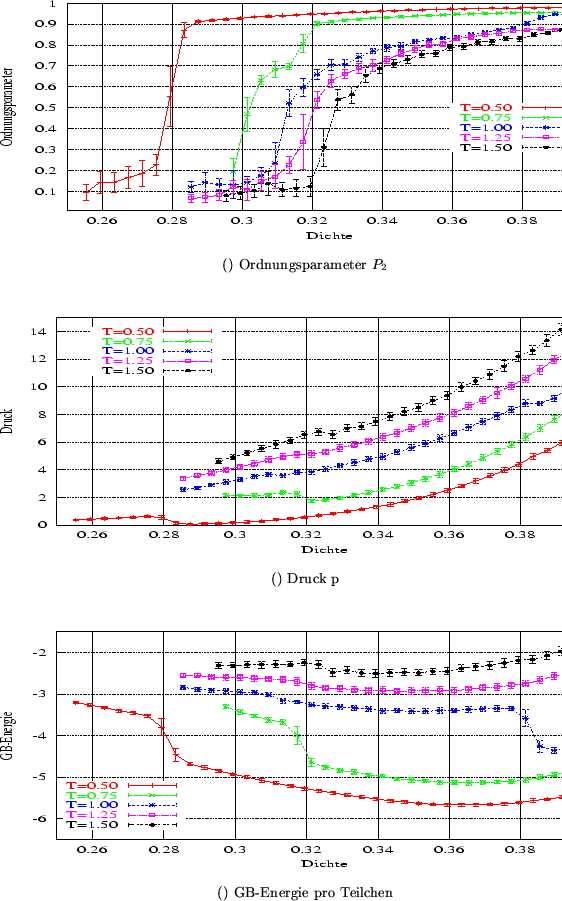
Der Verlauf des Ordnungsparameters bei der Kompression (Abbildung 3.20
(a) auf Seite ![[*]](cross_ref_motif.gif) ) weist bei allen Temperaturen auf einen
Phasenübergang hin. Der Verlauf ist ähnlich bei allen bearbeiteten
Temperaturen: es gibt einen steilen Anstieg des Ordnungsparameters bis zu dem
Wert im Bereich von 0.7 bis 0.8, dann vergrössert sich P2 noch immer zum
Wert 1, aber nicht mehr so schnell. Der Druck steigt bei allen
Temperaturen an (b), nur im Bereich des Überganges gibt es wieder wie bei der
Länge 3.0 ein lokales Minimum. Besonders bei der Temperatur 1.25 ist bei der
Dichte um 0.3 noch ein zweites Minimum zu sehen. Der Druck bei der
Temperatur 0.50 ist extrem niedrig - um Null. Bei der Energie des Systems
(Abbildung 3.20 (c) auf Seite
) weist bei allen Temperaturen auf einen
Phasenübergang hin. Der Verlauf ist ähnlich bei allen bearbeiteten
Temperaturen: es gibt einen steilen Anstieg des Ordnungsparameters bis zu dem
Wert im Bereich von 0.7 bis 0.8, dann vergrössert sich P2 noch immer zum
Wert 1, aber nicht mehr so schnell. Der Druck steigt bei allen
Temperaturen an (b), nur im Bereich des Überganges gibt es wieder wie bei der
Länge 3.0 ein lokales Minimum. Besonders bei der Temperatur 1.25 ist bei der
Dichte um 0.3 noch ein zweites Minimum zu sehen. Der Druck bei der
Temperatur 0.50 ist extrem niedrig - um Null. Bei der Energie des Systems
(Abbildung 3.20 (c) auf Seite ![[*]](cross_ref_motif.gif) ) gibt es ein lokales
Minimum nur bei der Temperatur 0.5. Sonst wurde nur ein plötzlicher Abfall der Energie vermerkt, der wieder
auf den Übergang hinweist. Bei der Temperaturen 1.00 und 1.25 ist besonders
ausgeprägt der zweite Abfall, der auf einen N-Sm Übergang hinweist.
) gibt es ein lokales
Minimum nur bei der Temperatur 0.5. Sonst wurde nur ein plötzlicher Abfall der Energie vermerkt, der wieder
auf den Übergang hinweist. Bei der Temperaturen 1.00 und 1.25 ist besonders
ausgeprägt der zweite Abfall, der auf einen N-Sm Übergang hinweist.
Abbildung:
Ordnungsparameter, Druck und Energie für den Reinstoff der Länge 3.5.
![\begin{figure}
\begin{center}
\subfigure [Ordnungsparameter $P_2$]{\mbox{\epsfig...
...le=fig/l35u.ps,
height=14cm, width=5.5cm, angle=270}}}
\end{center}\end{figure}](img130.gif) |
Das Wesentliche des Überganges findet in einem schmalen Bereich der Dichte statt
(Tabelle 3.4 auf Seite ![[*]](cross_ref_motif.gif) ). Bei einer höheren
Temperatur liegt der Übergang wieder im höheren Dichtebereich. P2 steigt
in einem Intervall der Dichte
). Bei einer höheren
Temperatur liegt der Übergang wieder im höheren Dichtebereich. P2 steigt
in einem Intervall der Dichte
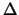
 = 0.2 von unter 0.2 über 0.7.
Dabei ist es interessant, dass die Übergänge bei den Temperaturen 1.0 und
1.25 fast gleiche Charakteristik aufweisen, und zwar mit zwei Übergängen (I-N
und N-Sm). In den P2 Graphen ist der N-Sm Übergang nicht so deutlich, doch die
Graphen für Druck und vor allem Energie weisen eindeutig auf den Übergang hin.
Bei den Temperaturen 0.5 und 0.75 es gibt nur einen I-Sm Übergang mit einem
breiten Dichtebereich, in dem sich die smektische Schichten bilden. Bei der
Temperatur 1.5 wurde nur ein I-N Übergang verzeichnet.
= 0.2 von unter 0.2 über 0.7.
Dabei ist es interessant, dass die Übergänge bei den Temperaturen 1.0 und
1.25 fast gleiche Charakteristik aufweisen, und zwar mit zwei Übergängen (I-N
und N-Sm). In den P2 Graphen ist der N-Sm Übergang nicht so deutlich, doch die
Graphen für Druck und vor allem Energie weisen eindeutig auf den Übergang hin.
Bei den Temperaturen 0.5 und 0.75 es gibt nur einen I-Sm Übergang mit einem
breiten Dichtebereich, in dem sich die smektische Schichten bilden. Bei der
Temperatur 1.5 wurde nur ein I-N Übergang verzeichnet.
Tabelle:
Das Intervall der Dichte des Überganges für den
Reinstoff der Länge 3.5.
| Temperatur |
Dichte (I-N) |
Dichte (I-Sm) |
Dichte (N-Sm) |
| 0.5 |
- |
0.18-0.023 |
- |
| 0.75 |
- |
0.22-0.24 |
- |
| 1.0 |
0.23-0.25 |
- |
0.28-0.29 |
| 1.25 |
0.24-0.26 |
- |
0.29-0.30 |
| 1.5 |
0.24-0.26 |
- |
- |
|
Die Graphen der Korrelationen nach den Übergängen (Abbildung 3.5 auf Seite
![[*]](cross_ref_motif.gif) ) zeigen ausgeprägte Schichten bei allen Temperaturen
ausser T=1.50. Wieder sind die Longitudinal-Paarkorrelationsfunktionen
gl(r) diejenigen, die auf die Bildung von Schichten mit einem Abstand um oder
etwas über 3 hinweisen. Je niedriger die Temperatur, desto grösser die
Orientierungsordnung. Die Graphen auf der linken Seite
(Translations- Paarkorrelationsfunktionen) sind den Graphen auf der rechten
Seite (Orientierungs- Paarkorrelationsfunktionen) sehr ähnlich, was auf
bestimmte Orientierung in der Richtung des Direktors hinweist. Bei T=1.50 sind
interessanterweise die Transversal-Korrelationen deutlicher als die
Longitudinal-Korrelationen. Das System ist bei einer hohe Dichte in der
nematische Phase, was sich in der
Ordnung senkrecht zum Direktor widerspiegelt.
Der Abstand für diese Länge (3.5) ist
günstig (3.5) nur bei der niedrigsten Temperatur (0.50). Sonst sind die
Schichten nicht mehr in idealem Abstand, was dann eine Abstossung
hervorbringt.
) zeigen ausgeprägte Schichten bei allen Temperaturen
ausser T=1.50. Wieder sind die Longitudinal-Paarkorrelationsfunktionen
gl(r) diejenigen, die auf die Bildung von Schichten mit einem Abstand um oder
etwas über 3 hinweisen. Je niedriger die Temperatur, desto grösser die
Orientierungsordnung. Die Graphen auf der linken Seite
(Translations- Paarkorrelationsfunktionen) sind den Graphen auf der rechten
Seite (Orientierungs- Paarkorrelationsfunktionen) sehr ähnlich, was auf
bestimmte Orientierung in der Richtung des Direktors hinweist. Bei T=1.50 sind
interessanterweise die Transversal-Korrelationen deutlicher als die
Longitudinal-Korrelationen. Das System ist bei einer hohe Dichte in der
nematische Phase, was sich in der
Ordnung senkrecht zum Direktor widerspiegelt.
Der Abstand für diese Länge (3.5) ist
günstig (3.5) nur bei der niedrigsten Temperatur (0.50). Sonst sind die
Schichten nicht mehr in idealem Abstand, was dann eine Abstossung
hervorbringt.
Die Teilchen der Länge 3.5 haben bei den Temperaturen 0.5 und 0.75 nur einen
isotropisch-smektischen Übergang, bei den Temperaturen 1.00 und 1.25 gibt es
zwei Übergänge (isotropisch-nematisch und nematisch-smektisch) und bei der
Temperatur 1.25 gibt es wieder nur einen isotropisch-nematischen Übergang.
Abbildung:
Korrelationsfunkt. für den Reinstoff der
Länge 3.5 nach dem Übergang.
|



Nächste Seite: Teilchen der Länge 4.0
Aufwärts: GB-Reinstoffe
Vorherige Seite: Teilchen der Länge 3.0
Inhalt
Renato Lukac
2000-01-02
![[*]](cross_ref_motif.gif) ). Für die E-Konfiguration liegt das Minimum bei dem
Abstand 3.62 und beträgt -0.378. Das ist fast 20 mal tiefer als das
Potential für die T-Konfiguration (-0.021), mehr als 100 mal tiefer als die
S-Konfiguration (-0.003) und die X-Konfiguration (-0.002) und zwar bei dem
Abstand 3.62. Bei dem Abstand 2.70 beträgt das Minimum für die
T-Konfiguration -0.382. Das Potential ist dort ungefähr 20 mal, bzw.
40 mal tiefer als die übrigen zwei Orientierungen (S-Konfiguration:
-0.020, X-Konfiguration: -0.010), die aber ihre Minima bei dem Abstand 1.12
haben (X-Konfiguration -1.00 und S-Konfiguration -1.893). Wenn wir nur die
Tiefe der Minima vergleichen, dann sehen wir, dass die Minima der S- und
X-Konfiguration 2.5 bis zu 5 mal grösser sind als die Minima der E- und
T-Konfiguration, wobei die letzten zwei fast gleich sind (S/X=1.89, S/T=4.96,
S/E=5.00, X/T=2.62, X/E=2.64, T/E=1.01).
). Für die E-Konfiguration liegt das Minimum bei dem
Abstand 3.62 und beträgt -0.378. Das ist fast 20 mal tiefer als das
Potential für die T-Konfiguration (-0.021), mehr als 100 mal tiefer als die
S-Konfiguration (-0.003) und die X-Konfiguration (-0.002) und zwar bei dem
Abstand 3.62. Bei dem Abstand 2.70 beträgt das Minimum für die
T-Konfiguration -0.382. Das Potential ist dort ungefähr 20 mal, bzw.
40 mal tiefer als die übrigen zwei Orientierungen (S-Konfiguration:
-0.020, X-Konfiguration: -0.010), die aber ihre Minima bei dem Abstand 1.12
haben (X-Konfiguration -1.00 und S-Konfiguration -1.893). Wenn wir nur die
Tiefe der Minima vergleichen, dann sehen wir, dass die Minima der S- und
X-Konfiguration 2.5 bis zu 5 mal grösser sind als die Minima der E- und
T-Konfiguration, wobei die letzten zwei fast gleich sind (S/X=1.89, S/T=4.96,
S/E=5.00, X/T=2.62, X/E=2.64, T/E=1.01).

 (3/1/2) ein. Das System hat
eine isotrope
(
(3/1/2) ein. Das System hat
eine isotrope
( (1/0/3). Wenn die Kompression zu rasch durchgeführt wird,
dann kann sich dieser Prozess nicht einstellen. Bei einer höheren Temperatur
geschieht der Übergang bei einer höheren Dichte, daher ist der Abstand
zwischen den Schichten kleiner - die Schichten wurden näher aneinander
gepresst. Bei einer genügend hohen Temperatur würde der Abstand dann zu
klein. Die Abstossung zwischen den Schichten würde zu gross, deswegen gibt es
einen anderen Kompromiss, bei dem es keine Schichten gibt.
(1/0/3). Wenn die Kompression zu rasch durchgeführt wird,
dann kann sich dieser Prozess nicht einstellen. Bei einer höheren Temperatur
geschieht der Übergang bei einer höheren Dichte, daher ist der Abstand
zwischen den Schichten kleiner - die Schichten wurden näher aneinander
gepresst. Bei einer genügend hohen Temperatur würde der Abstand dann zu
klein. Die Abstossung zwischen den Schichten würde zu gross, deswegen gibt es
einen anderen Kompromiss, bei dem es keine Schichten gibt.
![\begin{figure}
\begin{center}
\subfigure [T=0.50, $\rho=$\ 0.17]
{\mbox{\epsfig ...
...{\mbox{\epsfig {file=fig/l35t150r031.ps, width=4.5cm}}}
\end{center}\end{figure}](img129.gif)
![\begin{figure}
\begin{center}
\subfigure [Ordnungsparameter $P_2$]{\mbox{\epsfig...
...le=fig/l35u.ps,
height=14cm, width=5.5cm, angle=270}}}
\end{center}\end{figure}](img130.gif)