
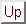


Nächste Seite: Teilchen der Länge 3.0
Aufwärts: GB-Reinstoffe
Vorherige Seite: Teilchen der Länge 2.0
Inhalt
Teilchen der Länge 2.5
Die Länge 2.5 ist besser geeignet für die Darstellung von FK als die früher
angewandten Längen 1.5 und 2.0. Die Minima des Potentials für die E- und
T-Konfiguration sind bei einem bestimmten Abstand deutlich unter den anderen
zwei Kurven (Abbildung 3.9 auf Seite ![[*]](cross_ref_motif.gif) ). Für die
E-Konfiguration liegt das Minimum bei dem Abstand 2.62 und beträgt -0.29. Das
ist mehr als fünfmal tiefer als das Potential für die T-Konfiguration
(-0.06), mehr als zwanzigmal tiefer als die S-Konfiguration (-0.018) und die
X-Konfiguration
). Für die
E-Konfiguration liegt das Minimum bei dem Abstand 2.62 und beträgt -0.29. Das
ist mehr als fünfmal tiefer als das Potential für die T-Konfiguration
(-0.06), mehr als zwanzigmal tiefer als die S-Konfiguration (-0.018) und die
X-Konfiguration
(- 0.012) und zwar bei dem Abstand 2.62. Bei dem Abstand 2.03
beträgt das Minimum für die T-Konfiguration (-0.38). Das Potential ist dort
ungefähr sechsmal tiefer als die übrigen zwei Orientierungen
(S-Konfiguration: -0.082, X-Konfiguration: -0.056), die aber ihre Minima bei
dem Abstand 1.12 haben (X-Konfiguration -1.00 und S-Konfiguration -1.45). Wenn
wir nur die Tiefe der Minima vergleichen, dann sehen wir, dass die Minima der
S- und X-Konfiguration 2.5- bis zu fünfmal grösser sind als die Minima der E-
und T-Konfiguration (S/X=1.45, S/T=3.82, S/E=5, X/T=2.63, X/E=3.45, T/E=1.31).
Die ausgeprägten Minima können bei genügend langsamer
Kompression/Dekompression des Systems eine entscheidende Rolle spielen.
'Genügend langsam' bedeutet, dass die MC-Schritte entsprechend klein sind
und dass es dazwischen immer viele Thermalisierungen gibt, die dann eine
Anpassung der Verteilung und der Orientierung der Teilchen hinsichtlich des
angewandtes Potentials, der Temperatur und der Dichte möglich machen, worin
auch der Hauptgrund unserer Langsamkeit der Simulation liegt.
Abbildung:
GB Potential für den Reinstoff der Länge 2.5.
 |
Die Anfangsdichte des Systems war  = 0.2. Es wurde thermalisiert bei der
Temperatur 1.25 und danach wurde es komprimiert bis zur Dichte 0.55. Mit dem
Zwischenergebnis bei
= 0.2. Es wurde thermalisiert bei der
Temperatur 1.25 und danach wurde es komprimiert bis zur Dichte 0.55. Mit dem
Zwischenergebnis bei  = 0.25 wurde in zwei Richtungen simuliert: das erste
System wurde gekühlt bis T=0.5, das zweite wurde erhitzt bis T=1.5. Dann
folgte wieder eine Kompression bei den Temperaturen T=0.5, T=0.75, T=1.0 und
T=1.5 bis maximal
= 0.25 wurde in zwei Richtungen simuliert: das erste
System wurde gekühlt bis T=0.5, das zweite wurde erhitzt bis T=1.5. Dann
folgte wieder eine Kompression bei den Temperaturen T=0.5, T=0.75, T=1.0 und
T=1.5 bis maximal  = 0.6.
= 0.6.
Die Visualisierung bei der Temperatur 0.5 zeigt die Bildung von Schichten nach
dem Übergang ( Abbildung 3.10 auf Seite ![[*]](cross_ref_motif.gif) ). Die
Teilchen bilden bei niedrigerer Dichte (
). Die
Teilchen bilden bei niedrigerer Dichte ( = 0.36) kleine Domänen (a), wobei
der Ordnungsparameter unter 0.2 bleibt. Mit der Kompression verkleinert sich
der verfügbare Raum für die Domänen und bei bestimmter Dichte (
= 0.36) kleine Domänen (a), wobei
der Ordnungsparameter unter 0.2 bleibt. Mit der Kompression verkleinert sich
der verfügbare Raum für die Domänen und bei bestimmter Dichte ( = 0.39)
trifft im System eine globale Ordnung ein (b). Der Ordnungsparameter steigt
dabei auf ungefähr 0.6. Mit weiterer Kompression bis zur Dichte 0.41 bilden
sich 7 Schichten aus (c), wobei der Direktor die frühere Orientierung
= 0.39)
trifft im System eine globale Ordnung ein (b). Der Ordnungsparameter steigt
dabei auf ungefähr 0.6. Mit weiterer Kompression bis zur Dichte 0.41 bilden
sich 7 Schichten aus (c), wobei der Direktor die frühere Orientierung
 = (0.05, 0.95, - 0.31) erhält. Der Ordnungsparameter steigt wieder bis den Wert
ungefähr 0.9. Die Schichtung ist klar zu sehen, wenn wir nur die Positionen
der Teilchenschwerpunkte darstellen (d). Zur weiteren Verdeutlichung wird in
(e) eine einzige Schicht mit 103 Teilchen dargestellt. Das System wurde
gedreht, damit wir die Schicht aus einer senkrechten Perspektive betrachten
können (f). Die Ordnung innerhalb der Schicht ist wieder klarer zu sehen, wenn
wir nur die Teilchenschwerpunkte darstellen (g). Es gibt eine 'schwache'
hexagonale Struktur. Ähnlich ist es auch bei der Temperatur 0.75.
= (0.05, 0.95, - 0.31) erhält. Der Ordnungsparameter steigt wieder bis den Wert
ungefähr 0.9. Die Schichtung ist klar zu sehen, wenn wir nur die Positionen
der Teilchenschwerpunkte darstellen (d). Zur weiteren Verdeutlichung wird in
(e) eine einzige Schicht mit 103 Teilchen dargestellt. Das System wurde
gedreht, damit wir die Schicht aus einer senkrechten Perspektive betrachten
können (f). Die Ordnung innerhalb der Schicht ist wieder klarer zu sehen, wenn
wir nur die Teilchenschwerpunkte darstellen (g). Es gibt eine 'schwache'
hexagonale Struktur. Ähnlich ist es auch bei der Temperatur 0.75.
Bei den Temperaturen 1.00, 1.25 und 1.50 sieht es anders aus: obwohl der
Ordnungsparameter bis zu einem Wert von ungefähr 0.9 steigt, gibt es dabei
keine deutliche Schichten. Das System bei der Temperatur 1.00 und der Dichte
0.49 hat P2=0.86 und den Direktor
 = (0.053, 0.950, - 0.308) (Abbildung
3.10 auf Seite
= (0.053, 0.950, - 0.308) (Abbildung
3.10 auf Seite ![[*]](cross_ref_motif.gif) ). Das System wurde aus allen
möglichen Perspektiven betrachtet, doch es war keine Schichtung zu sehen (h).
Wir haben wieder einen Teil des Systems genommen und ihn gedreht, damit
wir ihn aus einer senkrechten Perspektive betrachten können (i). Wir können
nur kurz reichende Raumordnung feststellen.
). Das System wurde aus allen
möglichen Perspektiven betrachtet, doch es war keine Schichtung zu sehen (h).
Wir haben wieder einen Teil des Systems genommen und ihn gedreht, damit
wir ihn aus einer senkrechten Perspektive betrachten können (i). Wir können
nur kurz reichende Raumordnung feststellen.
Abbildung:
Schnappschüsse für den Reinstoff der Länge 2.5.
![\begin{figure}
\begin{center}
\subfigure [T=0.50, $\rho=$\ 0.36]
{\mbox{\epsfig ...
...box{\epsfig {file=fig/l25t100r049l1d.ps, width=4.5cm}}}
\end{center}\end{figure}](img119.gif) |
Auch der Ordnungsparameter weist bei allen untersuchten Temperaturen auf
einen Übergang hin (Abbildung 3.11 (a) auf Seite ![[*]](cross_ref_motif.gif) ).
Der Übergang findet in einem bestimmten Bereich der Dichte statt, der von
Temperatur abhängt (Tabelle 3.2 auf Seite
).
Der Übergang findet in einem bestimmten Bereich der Dichte statt, der von
Temperatur abhängt (Tabelle 3.2 auf Seite ![[*]](cross_ref_motif.gif) ). Bei
höherer Temperatur liegt der Übergang im höheren Dichtebereich. Der Verlauf
des Ordnungsparameters ist bei den Temperaturen 1.00, 1.25 und 1.50 ziemlich
gleich: er steigt in einem Bereich der Dichte
). Bei
höherer Temperatur liegt der Übergang im höheren Dichtebereich. Der Verlauf
des Ordnungsparameters ist bei den Temperaturen 1.00, 1.25 und 1.50 ziemlich
gleich: er steigt in einem Bereich der Dichte
 = 0.5 von unter 0.1
bis über 0.8; bis zum Wert 0.6 schnell, dann aber langsamer. Bei der
Temperatur 0.75 ist es ähnlich, nur dass eine Stufe im Dichtebereich 0.415 und
0.445 dazwischen liegt. Bei der Temperatur 0.5 ist der Anstieg des
Ordnungsparameters den Wert 0.3 langsamer, dann aber bis 0.9 steil. Wir haben
auch Simulationen mit wenigeren Thermalisierungen durchgeführt. Dabei wurde
der Anstieg des Ordnungsparameters geringer,
= 0.5 von unter 0.1
bis über 0.8; bis zum Wert 0.6 schnell, dann aber langsamer. Bei der
Temperatur 0.75 ist es ähnlich, nur dass eine Stufe im Dichtebereich 0.415 und
0.445 dazwischen liegt. Bei der Temperatur 0.5 ist der Anstieg des
Ordnungsparameters den Wert 0.3 langsamer, dann aber bis 0.9 steil. Wir haben
auch Simulationen mit wenigeren Thermalisierungen durchgeführt. Dabei wurde
der Anstieg des Ordnungsparameters geringer,
 wurde grösser.
Im Verlauf der Kompression steigt der Druck bei allen Temperaturen an
(Abbildung 3.11 (b) auf Seite
wurde grösser.
Im Verlauf der Kompression steigt der Druck bei allen Temperaturen an
(Abbildung 3.11 (b) auf Seite ![[*]](cross_ref_motif.gif) ), nur im Bereich des
Überganges ist die Veränderung des Druckes kleiner - es gibt eine Stufe
dazwischen. So ähnlich ist es auch bei der Energie des Systems (Abbildung
3.11 (c) auf Seite
), nur im Bereich des
Überganges ist die Veränderung des Druckes kleiner - es gibt eine Stufe
dazwischen. So ähnlich ist es auch bei der Energie des Systems (Abbildung
3.11 (c) auf Seite ![[*]](cross_ref_motif.gif) ), indem es dort lokale Minima
gibt, die auch auf eine globale Veränderung im System hinweisen. Diese Minima
sind deutlicher bei niedrigeren Temperaturen.
), indem es dort lokale Minima
gibt, die auch auf eine globale Veränderung im System hinweisen. Diese Minima
sind deutlicher bei niedrigeren Temperaturen.
Abbildung:
Ordnungsparameter, Druck und Energie für den Reinstoff der Länge 2.5.
![\begin{figure}
\begin{center}
\subfigure [Ordnungsparameter $P_2$]{\mbox{\epsfig...
...le=fig/l25u.ps,
height=14cm, width=5.5cm, angle=270}}}
\end{center}\end{figure}](img120.gif) |
Tabelle:
Das Intervall der Dichte des Überganges für den
Reinstoff der Länge 2.5.
| Temperatur |
Dichte |
| 0.5 |
0.36-0.39 |
| 0.75 |
0.40-0.45 |
| 1.0 |
0.41-0.46 |
| 1.25 |
0.43-0.48 |
| 1.5 |
0.45-0.49 |
|
Aus den Graphen der Korrelationen nach dem Übergang (Abbildung
3.3 auf Seite ![[*]](cross_ref_motif.gif) ) kann man entnehmen, dass
für die Schichtung und Raumordnung der Teilchen eine ausgeprägte
Entwicklung nur bei den zwei niedrigsten Temperaturen (0.5 und 0.75)
kennzeichnend ist. Die Paarkorrelationsfunktionen (a,b) zeigen, dass die ersten
Maxima bei den beiden niedrigsten Temperaturen doppelt so hoch sind wie bei den
anderen Temperaturen. Die Oszillationen bei den beiden niedrigsten Temperaturen
weisen auf eine weitreichende Raumordnung hin. Dagegen werden bei den anderen
Temperaturen die Oszillationen nach den ersten Maxima bald flacher. Die
Longitudinal-Paarkorrelationsfunktionen (c,d) zeigen sehr ausgeprägte
Oszillationen für T=0.5 und T=0.75, die deutlich auf Schichten hinweisen.
Dagegen sind für andere Temperaturen keine wesentliche Oszillationen zu
vermerken. Die Longitudinal-Paarkorrelationsfunktionen sind konstant um den
Wert 1, die Longitudinal-Orientierungs-Paarkorrelationsfunktionen etwas unter
dem Wert des Ordnungsparameters. Auch die
Transversal-Paarkorrelationsfunktionen (e,f) zeigen ausgeprägte Raumordnung
innerhalb der Schichten für T=0.5 und T=0.75.
) kann man entnehmen, dass
für die Schichtung und Raumordnung der Teilchen eine ausgeprägte
Entwicklung nur bei den zwei niedrigsten Temperaturen (0.5 und 0.75)
kennzeichnend ist. Die Paarkorrelationsfunktionen (a,b) zeigen, dass die ersten
Maxima bei den beiden niedrigsten Temperaturen doppelt so hoch sind wie bei den
anderen Temperaturen. Die Oszillationen bei den beiden niedrigsten Temperaturen
weisen auf eine weitreichende Raumordnung hin. Dagegen werden bei den anderen
Temperaturen die Oszillationen nach den ersten Maxima bald flacher. Die
Longitudinal-Paarkorrelationsfunktionen (c,d) zeigen sehr ausgeprägte
Oszillationen für T=0.5 und T=0.75, die deutlich auf Schichten hinweisen.
Dagegen sind für andere Temperaturen keine wesentliche Oszillationen zu
vermerken. Die Longitudinal-Paarkorrelationsfunktionen sind konstant um den
Wert 1, die Longitudinal-Orientierungs-Paarkorrelationsfunktionen etwas unter
dem Wert des Ordnungsparameters. Auch die
Transversal-Paarkorrelationsfunktionen (e,f) zeigen ausgeprägte Raumordnung
innerhalb der Schichten für T=0.5 und T=0.75.
Die Teilchen der Länge 2.5 haben bei den Temperaturen T=0.5 und T=0.75
einen isotropisch-smektischen Übergang. Bei den Temperaturen T=1.00, T=1.25
und T=1.50 gibt es einen isotropisch-nematischen Übergang.
Abbildung:
Korrelationsfunkt. für den Reinstoff der
Länge 2.5 nach dem Übergang.
|



Nächste Seite: Teilchen der Länge 3.0
Aufwärts: GB-Reinstoffe
Vorherige Seite: Teilchen der Länge 2.0
Inhalt
Renato Lukac
2000-01-02
![[*]](cross_ref_motif.gif) ). Für die
E-Konfiguration liegt das Minimum bei dem Abstand 2.62 und beträgt -0.29. Das
ist mehr als fünfmal tiefer als das Potential für die T-Konfiguration
(-0.06), mehr als zwanzigmal tiefer als die S-Konfiguration (-0.018) und die
X-Konfiguration
). Für die
E-Konfiguration liegt das Minimum bei dem Abstand 2.62 und beträgt -0.29. Das
ist mehr als fünfmal tiefer als das Potential für die T-Konfiguration
(-0.06), mehr als zwanzigmal tiefer als die S-Konfiguration (-0.018) und die
X-Konfiguration 
![\begin{figure}
\begin{center}
\subfigure [T=0.50, $\rho=$\ 0.36]
{\mbox{\epsfig ...
...box{\epsfig {file=fig/l25t100r049l1d.ps, width=4.5cm}}}
\end{center}\end{figure}](img119.gif)
![\begin{figure}
\begin{center}
\subfigure [Ordnungsparameter $P_2$]{\mbox{\epsfig...
...le=fig/l25u.ps,
height=14cm, width=5.5cm, angle=270}}}
\end{center}\end{figure}](img120.gif)