Teilchen der Länge 2.0

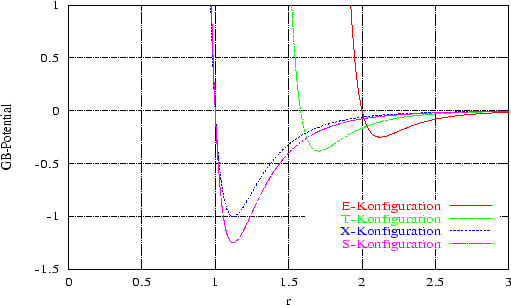
Auch die Länge 2.0 für die FK ist gering. Die Minima des Potentials für die E- und T-Konfiguration liegen bei einem bestimmten Abstand aber schon deutlich unter der anderen zwei Kurven (Abbildung 3.5 auf Seite

). Für die E-Konfiguration liegt das Minimum bei dem Abstand 2.12 und beträgt -0.25. Das ist mehr als doppelt so tief wie das Potential für die T-Konfiguration (-0.11), mehr als viermal tiefer als die S-Konfiguration (-0.055) und mehr als fünfmal tiefer als die X-Konfiguration (-0.045) bei dem Abstand 2.12. Bei einem dichteren System ist die E-Konfiguration dann wegen des hohen Potentials nicht mehr günstig. Bei dem Abstand 1.7 beträgt das Minimum für die T-Konfiguration (-0.38). Das Potential ist dort ungefähr doppelt so tief wie für die verbliebenen zwei Orientierungen (S-Konfiguration: -0.20, X-Konfiguration: -0.16), die aber ihre Minima bei dem Abstand 1.12 haben (X-Konfiguration, -1.00 S-Konfiguration -1.25). Wenn wir nur die Tiefe der Minima vergleichen, dann sehen wir, dass die Minima der S- und X-Konfiguration drei- bis fünfmal grösser sind als die Minima der E- und T-Konfiguration (S/E=5.0, S/T=3.30, S/X=1.25, X/T=2.63, X/E=4.0, T/E=1.52).

**Abbildung:** GB Potential für den Reinstoff der Länge 2.0.
$\begin{figure} \begin{center} {\mbox{\epsfig {file=fig/gb-pot.2.0.ps, width=7cm, height=12cm, angle=270}}} \end{center}\end{figure}$

Das System hatte wieder die Anfangsdichte 0.3064 und wurde bei der Temperatur 1.25 thermalisiert. Es wurde dann komprimiert bis zur Dichte 0.75. Mit dem Zwischenergebnis bei $\rho$ = 0.53 wurde in zwei Richtungen simuliert: das erste System wurde bis T=0.5 gekühlt, das zweite wurde bis T=1.5 erhitzt. Darauf folgte wieder eine Kompression bei den Temperaturen T=0.5, T=0.75, T=1.0 und T=1.5 bis zur Dichte 0.68.

Die Visualisierung (Abbildung 3.6 auf Seite

) zeigt für die Temperatur 0.5 wesentlich mehr Ordnung als bei dem System mit der Länge 1.5. Der erste Schnappschuss (a) wurde bei der Dichte 0.54 gemacht, wobei der Ordnungsparameter noch klein war (0.12). Der Druck war 5.03. Es gibt kleinere Domänen zu sehen. Mit der Kompression bis zur Dichte 0.56 wurde in die Simulationsbox mehr Orientierungsordnung gebracht, was sich an den Ordnungsparameter widerspiegelt (P₂ =0.57). Der Druck stieg bis 6.2, blieb aber im Normal-Bereich. Dem zweiten Schnappschuss (b) kann man entnehmen, dass durch die vielen Domänen eine globale Orientierung gebildet wurde, mit kleineren Domänen dazwischen. Mit weiterer Kompression bis zur Dichte 0.61 steigt der Ordnungsparameter noch bis P₂ =0.75, es gibt aber keine Schichten (typisch für smektische Phase) zu sehen. In dem dritten Schnappschuss (c) gibt es auch Teilchen zu sehen, die die Orientierung des Direktors nicht einbeschliessen. Der Druck stieg bis 10.82, was schon sehr hoch ist. 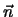Der Direktor blieb bei der Kompression von 0.56 bis 0.61 fast in der gleichen Richtung: $\vec{n}\,$ = (- 0.12, - 0.18, 0.98).

**Abbildung:** Schnappschüsse für den Reinstoff der Länge 2.0.
$\begin{figure} \begin{center} \subfigure [T=0.50, $\rho=$\ 0.54] {\mbox{\epsfig ... ... {\mbox{\epsfig {file=fig/l2t050r061.ps, width=4.5cm}}} \end{center}\end{figure}$

Der Ordnungsparameter ist für die Temperatur 1.5 unter 0.2 geblieben (Abbildung 3.7 (a) auf Seite

), obwohl das System extrem stark komprimiert wurde. Bei allen anderen inbegriffenen Temperaturen wurde ein Aufstieg des Ordnungsparameters bis über 0.7 verzeichnet. Der Übergang findet in einem bestimmten Bereich der Dichte statt (Tabelle 3.1 auf Seite

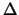
). Bei höherer Temperatur liegt der Übergang im höheren Dichtebereich. P₂ steigt in einem Intervall der Dichte $\Delta$ $\rho$ = 0.4 von unter 0.1 bis über 0.7. Im Verlauf der Kompression stieg der Druck monoton bei allen Temperaturen an (b). Im Übergangsbereich gibt es eine leichte Stufe. Auch der Verlauf der Energie (c) weist mit kleinen Minima auf einen Übergang hin. Die Energie stieg bei inbegriffenen Temperaturen und wurde bei den Temperaturen 1.25 und 1.5 sogar über die Null. Das wurde mit einem extrem dichteren System erreicht.

Tabelle: Das Intervall der Dichte des Hauptüberganges für den Reinstoff der Länge 2.0

Temperatur	Dichte
0.5	0.54-0.58
0.75	0.58-0.62
1.0	0.61-0.65
1.25	0.62-0.67
1.5	kein Übergang

**Abbildung:** Ordnungsparameter, Druck und Energie für den Reinstoff der Länge 2.0.
$\begin{figure} \begin{center} \subfigure [Ordnungsparameter $P_2$]{\mbox{\epsfig... ...ile=fig/l2u.ps, height=14cm, width=5.5cm, angle=270}}} \end{center}\end{figure}$

Die Korrelationen nach dem Übergang (Abbildung 3.2 auf Seite

) haben ähnlichen Verlauf der Kurven bei allen Temperaturen auser 1.5, bei der aber kein Übergang stattgefunden hat. Die Paarkorrelationsfunktion (a) hat für alle Temperaturen die erste Amplitude ungefähr 2, die zweite ist nur noch 1.2. Trotzt dem hohen Druck ist das überraschend kleine Raumordnung. Die Orientierungs - Paarkorrelationsfunktion (b) hat einen ähnlichen Verlauf, nur einen etwas niedrigeren. Bei T=1.5 ist sie fast gleich Null. Es gibt keine smektische Schichten, was die beide Longitudinalfunktionen (c,d) bestätigen. Die Transversal-Paarkorrelationsfunktionen (e,f) zeigen zwar weitreichende Korrelationen, die aber klein sind.

Die Teilchen der Länge 2 haben nur einen isotropisch-nematischen Übergang, der bei einem extrem grossem Druck stattfindet. Obwohl der Ordnungsparameter hoch war, blieb das System in der nematischen Phase.

**Abbildung:** Korrelationsfunkt. für den Reinstoff der Länge 2.0 nach dem Übergang.